在Shader编程里，frac 函数是一个极为常用的数学函数，它在多种图形效果的实现中发挥着重要作用。下面将详细介绍 frac 函数。

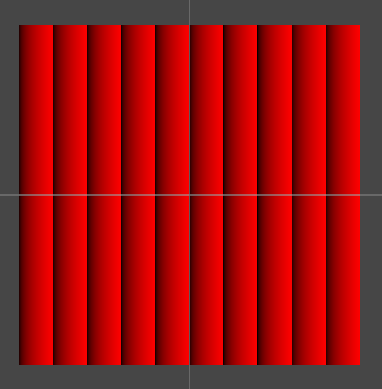
Shader "ShaderLearning/Shader08"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
    }
    SubShader
    {
        // No culling or depth
        Cull Off ZWrite Off ZTest Always

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            v2f vert(appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = v.uv;
                return o;
            }

            sampler2D _MainTex;

            fixed4 frag(v2f i) : SV_Target
            {
                float r = frac(i.uv.x * 10);
                return fixed4(r, 0, 0, 1);
            }
            ENDCG
        }
    }
}

功能

frac 函数的主要功能是返回一个数的小数部分。其数学原理为：对于给定的数 x，frac(x) 等同于 x - floor(x)，这里的 floor(x) 是取小于或等于 x 的最大整数。

语法

在不同的Shader语言中，frac 函数的使用方式基本一致。以下是一些常见Shader语言中的示例：

GLSL（OpenGL Shading Language）

float frac(float x);
vec2 frac(vec2 x);
vec3 frac(vec3 x);
vec4 frac(vec4 x);

HLSL（High-Level Shading Language）

float frac(float x);
float2 frac(float2 x);
float3 frac(float3 x);
float4 frac(float4 x);

示例代码

以下是一个简单的GLSL示例，展示了 frac 函数的使用：

#version 330 core

out vec4 FragColor;

void main()
{
    // 定义一个浮点数
    float value = 3.14;

    // 使用frac函数获取小数部分
    float fractionalPart = frac(value);

    // 输出小数部分
    FragColor = vec4(fractionalPart, fractionalPart, fractionalPart, 1.0);
}

应用场景

• 纹理动画：借助 frac 函数可以实现纹理的循环滚动效果。比如，在纹理坐标上加上一个随时间变化的值，再使用 frac 函数处理，这样纹理就会循环滚动。
• 噪声生成：在生成噪声纹理时，frac 函数可用于确保随机值处于 [0, 1] 区间内。
• 颜色渐变：frac 函数能用于创建周期性的颜色渐变效果。

注意事项

• frac 函数的输入参数可以是标量、向量，函数会对向量的每个分量分别进行处理。
• 由于浮点数精度的问题，在使用 frac 函数时可能会出现一些微小的误差。